Algorithm
[Algorithm] 완전탐색 (BruteForce)
걸어가는 신사
2022. 1. 21. 00:43
완전탐색 (BruteForce)
문제를 해결하기 위해 확인해야 하는 모든 경우를 전부 탐색하는 방법
- 모든 코테 문제에서 기본적으로 접근해 봐야 한다.
- 완전 탐색 문제를 접근할 때 중복과 순서를 신경써서 구현해야 한다.
1. 중복 O, 순서 O
(1) 문제
15651번: N과 M (3)
한 줄에 하나씩 문제의 조건을 만족하는 수열을 출력한다. 중복되는 수열을 여러 번 출력하면 안되며, 각 수열은 공백으로 구분해서 출력해야 한다. 수열은 사전 순으로 증가하는 순서로 출력해
www.acmicpc.net
- 1부터 N까지 자연수 중에서 M개를 고른 수열
- ex) N=4, M=2
- (1 1), (1 2), (1 3), (1 4)
- (2 1), (2 2), (2 3), (2 4)
- (3 1), (3 2), (3 3), (3 4)
- (4 1), (4 2), (4 3), (4 4)
(2) 시간, 공간복잡도 계산
- 입력
- 자연수 N과 M이 주어진다. (1 ≤ M ≤ N ≤ 7)

(3) 구현
public class S3_15651 {
static StringBuilder sb = new StringBuilder();
static int N, M;
static int[] selected;
public static void main(String[] args) throws IOException {
BufferedReader br = new BufferedReader(new InputStreamReader(System.in));
StringTokenizer st;
String str = br.readLine();
st = new StringTokenizer(str, " ");
N = Integer.parseInt(st.nextToken());
M = Integer.parseInt(st.nextToken());
selected = new int[N+1];
rec_func(1);
System.out.println(sb);
}
static void rec_func(int k) {
if (k == M+1) {
for (int i = 1; i <=M; i++) {
sb.append(selected[i]).append(" ");
}
sb.append("\n");
} else {
for (int i = 1; i <= N ; i++) {
selected[k] = i;
rec_func(k+1);
selected[k] = 0;
}
}
}
}
2. 중복 X, 순서 O => 순열(Permutation)
(1) 문제
15649번: N과 M (1)
한 줄에 하나씩 문제의 조건을 만족하는 수열을 출력한다. 중복되는 수열을 여러 번 출력하면 안되며, 각 수열은 공백으로 구분해서 출력해야 한다. 수열은 사전 순으로 증가하는 순서로 출력해
www.acmicpc.net
- 1부터 N까지 자연수 중에서 중복 없이 M개를 고른 수열
- ex) N=4, M=2
- (1 2), (1 3), (1 4)
- (2 1), (2 3), (1 4)
- (3 1), (3 2), (3 4)
- (4 1), (4 2), (4 3)
(2) 시간, 공간복잡도 계산
- 입력
- 자연수 N과 M이 주어진다. (1 ≤ M ≤ N ≤ 8)
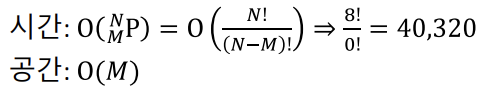
(3) 구현
public class S3_15649 {
static StringBuilder sb = new StringBuilder();
static int N;
static int M;
static int[] selected;
static boolean used[];
public static void main(String[] args) throws IOException {
BufferedReader br = new BufferedReader(new InputStreamReader(System.in));
StringTokenizer st;
String str = br.readLine();
st = new StringTokenizer(str, " ");
N = Integer.parseInt(st.nextToken());
M = Integer.parseInt(st.nextToken());
selected = new int[M+1];
used = new boolean[N+1];
rec_func(1);
System.out.println(sb);
}
static void rec_func(int k) {
if(k==M+1) {
for (int i = 1; i <=M; i++) {
sb.append(selected[i]).append(" ");
}
sb.append("\n");
} else {
for (int i = 1; i <=N; i++) {
if(!used[i]) {
selected[k] = i;
used[i] = true;
rec_func(k+1);
selected[k] = 0;
used[i] = false;
}
}
}
}
}
3. 중복 O, 순서 X
(1) 문제
15652번: N과 M (4)
한 줄에 하나씩 문제의 조건을 만족하는 수열을 출력한다. 중복되는 수열을 여러 번 출력하면 안되며, 각 수열은 공백으로 구분해서 출력해야 한다. 수열은 사전 순으로 증가하는 순서로 출력해
www.acmicpc.net
- 1부터 N까지 자연수 중에서 M개를 고른 수열
- 같은 수를 여러 번 골라도 된다.
- 고른 수열은 비내림차순이어야 한다.
- 길이가 K인 수열 A가 A1 ≤ A2 ≤ ... ≤ AK-1 ≤ AK를 만족하면, 비내림차순이다.
- ex) N=4, M=2
- (1 1), (1 2), (1 3), (1 4)
- (2 2), (2 3), (2 4)
- (3 3), (3 4)
- (4 4)
(2) 시간, 공간복잡도 계산
- 입력
- 자연수 N과 M이 주어진다. (1 ≤ M ≤ N ≤ 8)

(3) 구현
public class S3_15652 {
static StringBuilder sb = new StringBuilder();
static int N;
static int M;
static int[] selected;
public static void main(String[] args) throws IOException {
BufferedReader br = new BufferedReader(new InputStreamReader(System.in));
StringTokenizer st;
String str = br.readLine();
st = new StringTokenizer(str, " ");
N = Integer.parseInt(st.nextToken());
M = Integer.parseInt(st.nextToken());
selected = new int[M+1];
selected[0] = 1; //rec_func(1)이 실행될 때 반복문 초기값 설정을 위해 1을 넣어준다.
rec_func(1);
System.out.println(sb);
}
static void rec_func(int k) {
if(k == M+1) {
for (int i = 1; i <=M; i++) {
sb.append(selected[i]).append(" ");
}
sb.append("\n");
} else {
for (int i = selected[k-1]; i <=N; i++) {
selected[k] = i;
rec_func(k+1);
selected[k] = 0;
}
}
}
}
4. 중복X, 순서X => 조합(Combination)
(1) 문제
15650번: N과 M (2)
한 줄에 하나씩 문제의 조건을 만족하는 수열을 출력한다. 중복되는 수열을 여러 번 출력하면 안되며, 각 수열은 공백으로 구분해서 출력해야 한다. 수열은 사전 순으로 증가하는 순서로 출력해
www.acmicpc.net
- 1부터 N까지 자연수 중에서 중복 없이 M개를 고른 수열
- 고른 수열은 오름차순이어야 한다.
- ex) N=4, M=2
- (1 2), (1 3), (1 4)
- (2 3), (2 4)
- (3 4)
(2) 시간, 공간복잡도 계산
- 입력
- 자연수 N과 M이 주어진다. (1 ≤ M ≤ N ≤ 8)

(3) 구현
public class S3_15650 {
static StringBuilder sb = new StringBuilder();
static int N;
static int M;
static int[] selected;
static boolean[] visited;
public static void main(String[] args) throws IOException {
BufferedReader br = new BufferedReader(new InputStreamReader(System.in));
StringTokenizer st;
String str = br.readLine();
st = new StringTokenizer(str, " ");
N = Integer.parseInt(st.nextToken());
M = Integer.parseInt(st.nextToken());
selected = new int[M+1];
visited = new boolean[N+1];
selected[0] = 0;
rec_func(1);
System.out.println(sb);
}
static void rec_func(int k) {
if(k == M+1) {
for (int i = 1; i <=M; i++) {
sb.append(selected[i]).append(" ");
}
sb.append("\n");
} else {
for (int i = selected[k-1]+1; i <=N; i++) {
selected[k] = i;
rec_func(k+1);
selected[k] = 0;
}
}
}
}정리

- 완전 탐색 문제를 접근할 때
- 고를 수 있는 값의 종류 파악하기
- 중복을 허용하는지
- 순서가 중요한지
반응형